
Full Answer
What is the Ito formula used for stock price distribution?
A standard application is to use the Ito formula to derive the stock price distribution from the process of F = ln (5): Since and O are constant, F follows a generalized Wiener process with a constant drift a = X - Viti1 and diffusion with standard deviation c^lt.
What is Ito's formula in stochastic calculus?
Stochastic Calculus—Ito’s Formulaˆ In stochastic calculus, one must also keep the second-order terms. Equation (1) becomesIto’s formulaˆ, du=u′dx+ 1 2 u′′(dx)2(2) This equation isexact; the third-order and higher order terms are zero.
What is the Ito process in statistics?
The Ito process is a generalized Wiener process where the coefficients, a and b, are function of the underlying variable S and of the time t: Drift and variance are, respectively a {St, t)At and b {St, t)Az, with variance being bSt, t)At.
What is Ito’s lemma in calculus?
A. Ito’s lemma: Ito’s lemma gives a derivative chain rule of random variables. Let Gbe a function of (S;t). Ito’s lemma states that Gfollows the generalized Wiener process as follows: dG=
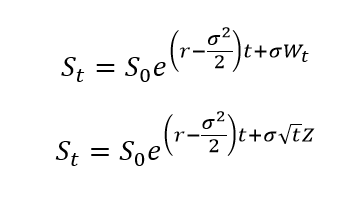
How do you use Ito's formula?
0:4111:28Ito's lemma, also known as Ito's formula, or Stochastic chain ruleYouTubeStart of suggested clipEnd of suggested clipWe can write it in integral form as follows.MoreWe can write it in integral form as follows.
Why do we use Ito's lemma?
The Ito's lemma provides a framework to differentiate the functions of stochastic process and this is of particular significance to derivative pricing (before Ito's work, people did not know how to do it). Ito's lemma allows us to derive the stochastic differential equation (SDE) for the price of derivatives.
Why are generalized Wiener processes inappropriate for stock prices?
It is tempting to suggest that a stock price follows a generalized Weiner process; that is, that is has a constant expected drift rate and a constant variance rate. However, this model fails to capture a key aspect of stock prices.
How do you use Ito's lemma?
2:5538:32Applications of Ito's Lemma - YouTubeYouTubeStart of suggested clipEnd of suggested clipAnd the way we calculate these is we take derivatives. And partial derivatives we take the partialMoreAnd the way we calculate these is we take derivatives. And partial derivatives we take the partial derivative of the new function that you've made up with respect to s.
How do you solve OU process?
2:5417:17Ornstein Uhlenbeck (OU) Process: solution, mean, variance ... - YouTubeYouTubeStart of suggested clipEnd of suggested clipThis equation is usually solved via the integrating factor method.MoreThis equation is usually solved via the integrating factor method.
Are stock prices stochastic?
Stock prices are stochastic processes in discrete time which take only discrete values due to the limited measurement scale. Nevertheless, stochastic processes in continuous time are used as models since they are analytically easier to handle than discrete models, e.g. the binomial or trinomial process.
What is Brownian motion in stochastic process?
Summary. Brownian motion is by far the most important stochastic process. It is the archetype of Gaussian processes, of continuous time martingales, and of Markov processes. It is basic to the study of stochastic differential equations, financial mathematics, and filtering, to name only a few of its applications.
Where time is measured in years if a 2 and B 3 What is the expected value after 3 years?
A variable x starts at 10 and follows the generalized Wiener process dx = a dt + b dz where time is measured in years. If a = 2 and b =3 what is the expected value after 3 years? the end of 3 years is 10+6 = 16.
What is Ito calculus used for?
Itô calculus, named after Kiyosi Itô, extends the methods of calculus to stochastic processes such as Brownian motion (see Wiener process). It has important applications in mathematical finance and stochastic differential equations.
How is Brownian motion used in finance?
Under this model, these assets have continuous prices evolving continuously in time and are driven by Brownian motion processes. This model requires an assumption of perfectly divisible assets and a frictionless market (i.e. that no transaction costs occur either for buying or selling).
What is called Brownian motion?
Brownian motion is the random motion of a particle as a result of collisions with surrounding gaseous molecules. Diffusiophoresis is the movement of a group of particles induced by a concentration gradient. This movement always flows from areas of high concentration to areas of low concentration.
How do you derive Ito Lemma?
7:1126:02Derivation of Ito's Lemma - YouTubeYouTubeStart of suggested clipEnd of suggested clipOkay plus the first derivative of the function and the derivative of the function with respect toMoreOkay plus the first derivative of the function and the derivative of the function with respect to the first variables that drew to the function respect to a and evaluate that at 0 0.
The Ito Process
The Ito process is a generalized Wiener process where the coefficients, a and b, are function of the underlying variable S and of the time t:
The Stock Price Process
For stock prices, the return is randomly distributed normally and i.i.d. because stock price returns are supposed to have a positive trend plus random deviations independent from past deviations, in line with the efficiency hypothesis of stock markets.
The Mean Reverting Process
A mean reverting process intends to model processes that cannot drift away of some long-term value by a large magnitude for long periods:
The "Rare Event" Process
The "jump process" is used to model rare events. Rare events are abnormal jumps of stock prices. In this text, rare events also include defaults which follow a jump process. Rare events occur unexpectedly and their probability of occurrence increases with the time interval elapsed.
Ito Lemma
The Ito lemma, which serves mainly for considering the stochastic processes of a function F (St, t) of a stochastic variable, following one of the standard stochastic processes, resolves the difficulty.
Example: Stock Price Distribution
A standard application is to use the Ito formula to derive the stock price distribution from the process of F = ln (5):
Who is paying for iTeos?
Britain's GlaxoSmithKline Plc has agreed to pay up to $2 billion to iTeos Therapeutics Inc to develop and sell a potential cancer treatment together, the companies said on Monday.
How much is iTeos upfront?
Boston-based iTeos, whose shares jumped 52% in premarket trading, will receive a $625 million upfront payment and is eligible to get up to $1.45 billion more if the programme meets certain development and commercial milestones.
The Ito Process
The Stock Price Process
- For stock prices, the return is randomly distributed normally and i.i.d. because stock price returns are supposed to have a positive trend plus random deviations independent from past deviations, in line with the efficiency hypothesis of stock markets. Under the efficiency hypothesis, the return reacts to innovations, not to past information, which...
The Mean Reverting Process
- A mean reverting process intends to model processes that cannot drift away of some long-term value by a large magnitude for long periods: Sdesignates here a process followed by a market parameter, typically an interest rate, not a stock price. Such a model is inconsistent with the market efficiency which implies that stock returns are independent from past returns. When S is …
The "Rare Event" Process
- The "jump process" is used to model rare events. Rare events are abnormal jumps of stock prices. In this text, rare events also include defaults which follow a jump process. Rare events occur unexpectedly and their probability of occurrence increases with the time interval elapsed. The size of the event is not small, as it is with the usual normal distribution, even when the time interval i…