What is the binomial option pricing model?
The binomial option pricing model is another popular method used for pricing options. 1 Assume there is a call option on a particular stock with a current market price of $100. The at-the-money (ATM) option has a strike price of $100 with time to expiry for one year.
What are fractional shares?
Textbook contributor. Personal finance writer. Passionate advocate of smart money moves to achieve financial success. Fractional shares are partial shares of a company's stock: Instead of owning one or more full shares of the stock, you own a portion, or fraction, of one.
What is the binomial theorem for fractional exponents?
Fractional Binomial Theorem. The binomial theorem for integer exponents can be generalized to fractional exponents. The associated Maclaurin series give rise to some interesting identities (including generating functions) and other applications in calculus. For example, f(x) = 1+x√ = (1+x)1/2 is not a polynomial.
What is the volatility of the binomial state of the price?
The volatility is already included by the nature of the problem's definition. Assuming two (and only two – hence the name “binomial”) states of price levels ($110 and $90), volatility is implicit in this assumption and included automatically (10% either way in this example).

Does stock price follow Brownian motion?
However, stock markets, the foreign exchange markets, commodity markets and bond markets are all assumed to follow Brownian motion, where assets are changing continually over very small intervals of time and the position, namely the change of state on the assets, is being al- tered by random amounts.
How do you calculate binomial pricing?
The cost today must be equal to the payoff discounted at the risk-free rate for one month. The equation to solve is thus: Option price = $50 - $45 x e ^ (-risk-free rate x T), where e is the mathematical constant 2.7183.
What is binomial option pricing model explain?
The Binomial Option Pricing Model is a risk-neutral method for valuing path-dependent options (e.g., American options). It is a popular tool for stock options evaluation, and investors use the model to evaluate the right to buy or sell at specific prices over time.
What is U and D in binomial tree?
u: The factor by which the price rises (assuming it rises). d: The factor by which the price falls (assuming it falls).
Why is the binomial option pricing model used to price options?
The binomial option pricing model is significant because it is easier to use than other models. You can compare the option price to the underlying stock prices of the option. It allows an investor to look at different periods for an option to the point of the expiration date.
Is Black-Scholes better than binomial?
While both the Black-Scholes model and the binomial model can be used to value options, the binomial model has a broader range of applications, is more intuitive, and is easier to use.
How do you do the binomial model?
How to Work a Binomial Distribution Formula: Example 2Step 1: Identify 'n' from the problem. ... Step 2: Identify 'X' from the problem. ... Step 3: Work the first part of the formula. ... Step 4: Find p and q. ... Step 5: Work the second part of the formula. ... Step 6: Work the third part of the formula.More items...
Who developed the binomial pricing model?
William SharpeThe binomial model was first proposed by William Sharpe in the 1978 edition of Investments (ISBN 013504605X), and formalized by Cox, Ross and Rubinstein in 1979 and by Rendleman and Bartter in that same year.
What are three option pricing models?
A three-tiered pricing model is a business method of laying out three different service solutions to your customers at three different pricing points, no matter if you use fixed pricing, value pricing or a volume pricing model.
How many steps are in a binomial tree?
In practice, the life of an option is divided into 30 or more time steps. In each step, there is a binomial stock price movement.
How do binomial trees work?
A binomial tree is a representation of the intrinsic values an option may take at different time periods. The value of the option at any node depends on the probability that the price of the underlying asset will either decrease or increase at any given node.
Is Monte Carlo a binomial model?
The goal of this lab is to create a computer simulation which generates data distributed according to the binomial distribution (known as a Monte Carlo simulation) and analyze the generated data to better understand the behavior of the binomial distribution in different limiting cases.
How do you do the binomial model?
How to Work a Binomial Distribution Formula: Example 2Step 1: Identify 'n' from the problem. ... Step 2: Identify 'X' from the problem. ... Step 3: Work the first part of the formula. ... Step 4: Find p and q. ... Step 5: Work the second part of the formula. ... Step 6: Work the third part of the formula.More items...
How do you do a two step binomial tree?
4:226:33Two Step Binomial Tree - European Call - YouTubeYouTubeStart of suggested clipEnd of suggested clipSo we're going to think about the middle of a slice. And here what we do is we treat each node inMoreSo we're going to think about the middle of a slice. And here what we do is we treat each node in the middle slice as having a single binomial tree to the right of it.
How many steps are in a binomial tree?
In practice, the life of an option is divided into 30 or more time steps. In each step, there is a binomial stock price movement.
What is binomial heap with example?
A Binomial Heap with n nodes has the number of Binomial Trees equal to the number of set bits in the binary representation of n. For example, let n be 13, there are 3 set bits in the binary representation of n (00001101), hence 3 Binomial Trees.
How is randomness of stock price modelled?
In the general accepted model, the randomness of stock price is modelled by Brownian motion process. A stock price process is represented by the stochastic differential equation (SDE) as shown in Note that the parameters and are the rate of return and the volatility, respectively. The process in ( 1) is a standard Brownian motion process. The stochastic differential equation ( 1) is driven by the Brownian motion process . In the real world, and in ( 1) are not constant at any time. Hence these parameters in the paper are the adaptable parameters based on time. In the paper, model ( 1) is called a Brownian motion model with adaptive parameters (BMAP).
When was the historical drift rate for closed prices predicted?
The historical drift rate for closed prices prediction from July 11, 2011, to July 8, 2013.
What are the two asset pricing models?
Two asset pricing models are presented in the paper. One is the Brownian motion model with adaptive parameters called BMAP and another one is the fractional Brownian motion model with adaptive parameters called FBMAP. The rate of return and volatility in both models are adaptive at any time. The driven process in the BMAP is Brownian motion, while the driven process in the FBMAP is a fractional Brownian motion. The BMAP and the FBMAP are applied to simulate the ADVANC and LH stock prices. The simulated prices from both models are compared with the empirical prices. The accuracy index ARPE is used in the paper. From the 10,000 scenarios of simulated prices of each model, the average and standard deviation of ARPE from both models show that the FBMAP provides a better appropriateness with the dataset than the BMAP in case of ADVANC and LH. Therefore, the FBMAP is suitable to predict the ADVANC and LH closed prices in the future.
What section of the paper is the BMAP and FBMAP?
The paper is organized as follows. Preliminaries on a fractional Brownian motion are given in Section 2. The estimation of the rate of return and volatility is shown in Section 3. In Section 4, the BMAP and the FBMAP are explained. Finally, Section 5 concludes the work in the paper.
How many scenarios are there in Brownian motion?
In general, the 10,000 scenarios or sample paths of Brownian motion process are considered. In each path, the ARPE is computed from both models. The comparison results between the BMAP and the FBMAP can be seen from Table 3. It can be seen that the average ARPE of the FBMAP is less than the average ARPE of the BMAP. Moreover, the standard deviation of ARPE from the FBMAP is smaller compared with the BMAP. The simulation results show that the FBMAP can provide the small ARPE compared with the BMAP in case of ADVANC and LH.
What is the ADVANC and LH stock price model?
The ADVANC and LH stock price models are studied by using fractional Brownian motion process to explain uncertainly behavior instead of Brownian motion process. The Brownian motion model with adaptive parameters (BMAP) and the fractional Brownian motion model with adaptive parameters (FBMAP) are presented to model the ADVANC and LH stock prices.
What is Brownian motion?
Therefore, the Brownian motion is usually used to model a stock price. However, Brownian motion process has the independent increments property. This means that the present price must not affect the future price. In fact, the present stock price may influence the price at some time in the future.
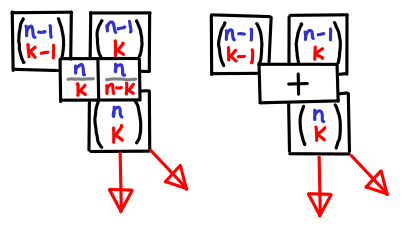
Binomial Theorem for Fractional Exponent
The above example generalizes immediately for all fractional exponents α \alpha α. Let α \alpha α be a real number and k k k a positive integer. Define
Examples
The binomial coefficients ( p / q k) \binom {p/q} {k} ( kp/q ) can sometimes be rewritten in interesting ways.